Research Design and Conceptual Framework

The project is designed in several strands: Document analysis (textbooks, policies, and course documents), surveys of departments and instructors, and assessment of students.

The project flow is shown in Figure 2 below:

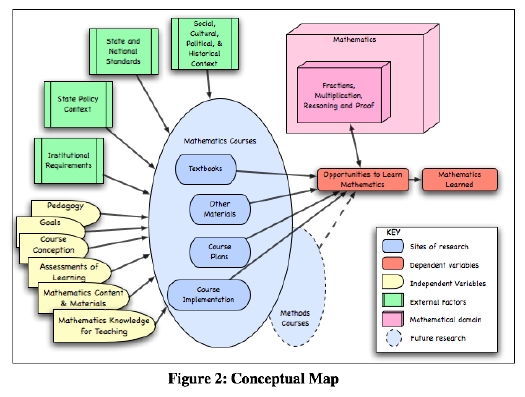
Our conceptual framework hinges on the concept of opportunity to learn, which we assess using data from the three surveys (of mathematics departments, instructors, and students.) This relates to fundamental questions of the research:

What do courses for prospective elementary teachers give them an opportunity to learn?
Are the classes giving them opportunities to learn what policy and research suggest are important for effective mathematics teaching?

As indicated in the diagram, we are not assessing all of the mathematics elementary teachers need to learn. Instead, we focus on three critical areas: fractions, multiplication, and reasoning and proof. These three areas were selected because they represent different cognitive and pedagogical aspects of elementary mathematics: fractions are numbers; multiplication is an operation; and reasoning and proof are ways of thinking about and doing mathematics. In addition, these three topics have been the subjects of research on mathematics teaching and student learning.

a. Fractions

Fractions is a topic that recurs in K-8 mathematics, beginning in about grade 3 and continuing through grades 6-8 depending on the curriculum. Wu (1999; 2005) argues that understanding fractions is critically important for the future study of algebra and more advanced mathematics and constitutes "students' first serious excursion into abstraction" (2005, p. 2). Fractions have been a source of trouble for elementary teachers and students, a topic that seems to be poorly understood and much maligned (e.g., Behr et al., 1983; Mack, 1990, 1995; Saxe et al., 2005) . Students may believe that operations on fractions are arbitrary and that the definition of a fraction changes depending on the context. They routinely fail to grasp the concept of a unit.

b. Multiplication

Multiplication is a different kind of topic in K-8 mathematics, an operation that is taught across grade levels from K-8 and appears in more complex versions as students' exposure to number systems expands. Multiplication is taught first with whole numbers and gradually extended to fractions, decimals, percents, integers and sometimes, algebraic expressions in the course of the K-8 curriculum. Research suggests that students often come away from early mathematical experiences believing that multiplication changes in different number systems (Lampert, 1986) . At the same time, they hold on to the misconception that "multiplication makes bigger" (e.g., Bell et al. , 1981)

c. Reasoning and Proof

Reasoning and proof is often taught implicitly if at all in K-8 mathematics (Ball et al., 2002) . Yet, because reasoning and proof are critical elements of learning mathematics, there is a growing appreciation of the idea that reasoning should be part of all students' mathematical experiences and across all grades (National Council of Teachers of Mathematics, 2000; Schoenfeld, 1994; Yackel & Hanna, 2003) . This places increased demands on K-8 teachers' understanding of reasoning and proof.

References

Ball, D. L., Hoyles, C., Jahnke, H. N., & Movshovitz-Hadar, N. (2002). The teaching of proof. In L. I. Tatsien (Ed.), Proceedings of the international congress of mathematicians (Vol. III). Beijing: Higher Education Press.

Behr, M. J., Lesh, R. A., Post, T. R., & Silver, E. A. (1983). Rational-number concepts. In R. A. Lesh & M. Landau (Eds.), Acquisition of mathematics concepts and processes (pp. 91-126). New York: Academic Press.

Bell, A., Swan, W., & Taylor, G. (1981). Choice of operation in verbal problems with decimal numbers. Educational Studies in Mathematics, 12 (399-420).

Lampert, M. (1986). Knowing, doing, and teaching multiplication. Cognition and Instruction, 3 (4), 305-342.

Mack, N. K. (1990). Learning fractions with understanding: Building on informatl knowledge. Journal for Research in Mathematics Education, 21 (1), 16-32.

Mack, N. K. (1995). Confounding whole-number and fraction concepts when building on informal knowledge. Journal for Research in Mathematics Education, 26 (5), 422-441.

National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics . Reston, VA: National Council of Teachers of Mathematics.

Saxe, G. B., Taylor, E. V., MacIntosh, C., & Gearhart, M. (2005). Representing fractions with standard notation: A developmental analysis.

Schoenfeld, A. H. (1994). What do we know about mathematics curricula? Journal of Mathematical Behavior, 13 , 55-80.

Wu, H.-H. (1999). Some remarks on the teaching of fractions in elementary school. from http://math.berkeley.edu/~wu/fractions2.pdf

Wu, H.-H. (2005, April). Key mathematical ideas in grades 5-8. Paper presented at the National Council of Teachers of Mathematics Research Presession. Anaheim, CA.

Yackel, E., & Hanna, G. (2003). Reasoning and proof. In J. Kilpatrick, W. G. Martin & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 227-236). Reston, VA: National Council of Teachers of Mathematics.

Updated 09/12/2009